Making a 3D Graphics Engine from Scratch

Posted on April 4, 2021 Updated on August 18, 2021 Comments are closed.

April 4, 2021

After completing my first project using a graphics library, I wanted to try my hand at making an actual game. It would be trivially easy to create 2D game with the plethora of beginner tools available to developers, so I wanted a bit more of a challenge. Something that held my fascination for a long time was 3D Tic Tac Toe. By adding just one more dimension to the simple children’s game, you can increase its complexity by an order of magnitude. In fact, I had made a 2D command line version of the game years before, although players found it somewhat hard to grasp as it was only a 2D representation of a 3D space. To overcome this, I would simply make it in 3D for real this time.

My original plan was to use an existing engine with all the heavy lifting for 3D graphics already taken care of. I downloaded Godot Mono and began to play around with it, but I found its level of abstraction to be somewhat unfulfilling. Having already taken both linear algebra and multivariable derivative calculus, I figured I had enough math knowledge to at least attempt to program a 3D graphics engine myself, especially given the fact that I would only have to draw simple cubes. Additionally, it was my spring break, so I had a full week to myself (barring work). So, I set off to get started.

The most fundamental thing that any programmer must understand before setting off into the wide world of 3D graphics is projection. No human being is capable of seeing the world as it truly is, nor is any computer monitor capable of displaying it. I don’t mean this in any sort of philosophical sense. As beings occupying a 3D space, our eyes can only ever see a 2D projection of a 3D space. This may sound a little confusing at first, so I’ll use a 2D world as an example. Imagine a 2D being, having only length and width. We will call him Mr. Flat. Mr. Flat’s world might look like this:

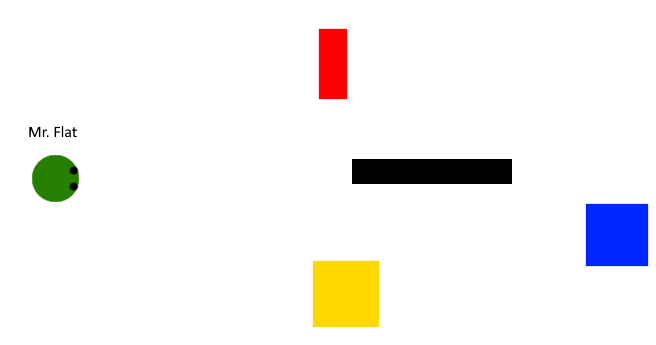
As three-dimensional beings, we are able to perceive Mr. Flat’s world in full 2D , however Mr. Flat cannot. Occupying a 2D space, Mr. Flat can only ever see a one-dimensional projection of his 2D world. In order to produce such a projection, we can imagine all the objects in Mr. Flat’s World at emitting beams of light in every direction. We will ignore all the beams that do not touch Mr. Flat’s eyes, and only consider one of Mr. Flat’s eyes for the sake of simplicity. Assuming Mr. Flat’s eye works like ours, the light from all these objects will enter a pinhole before being projected onto a surface that relays image data to his brain. This might look something like this:

By constraining the light rays that are allowed to hit Mr. Flat’s image detector through a single hole, we create a 1D projection of Mr Flat’s 2D space. Hence, this is how Mr. Flat sees his world:

Notice that this image is flipped 180 degrees from how Mr. Flat’s world really is. This is simply a function of how light enters the pinhole. If Mr. Flat is properly evolved to life in his 2D space, his brain would automatically flip this image for him, just like our brains do with our 3D projection. This is also a good way to illustrate how Mr. Flat could be able to resolve distance in his world. Although the blue cube is nearly the exact same size as the yellow cube, it appears smaller in the projection because of the fact that it is further away from the pinhole, and therefore there is a smaller angle between the rays of light that enter Mr. Flat’s eye.

While this 1D projection of a 2D world was simply an example before we move on to 3D space, it did find use in early computer graphics. If we assume that every object in the world has the same height, we can simply project a 2D world onto a 1D surface and add textures to give the player the illusion of a 2D projection of a 3D world. This can be seen in action most famously in Wolfenstein 3D (which with what we know now is really Wolfenstein 2D):

However, for our purposes of creating a general 3D graphics engine, we will need a full real 2D projection of a full 3D world, so we must say goodbye to Mr. Flat and enter the realm of linear algebra.

In order to apply this projection to 3D, we need to apply something called a camera transform. In order to perform our camera transform, we need the following information:

The position of the point we want to project \(p_{x,y,z}\)
The position of the camera’s pinhole \(c_{x,y,z}\)
The 3D orientation of the camera \(\theta _{x,y,z}\)
The position of the projection surface relative to the pinhole \(e_{x,y,z}\)

Now, this next bit is going to get a little complicated, but rest assured that it is the most complicated math that is required to make 3D work. First, we must transform the 3D point coordinates using the following transformation:

Now, we still have a problem in that the result of this transformation is still a 3D coordinate. In order to project this transformation onto the camera’s projection plane, we apply the comparatively simple formulae:

\(\Large b_x = \frac{e_z}{d_z}d_x + e_x\)

\(\Large b_y = \frac{e_z}{d_z}d_y + e_y\)

I implemented this in Python as follows:

def project(self, camera, xoffset, yoffset): #project point onto 2d camera plane (this formula from wikipedia.org/wiki/3D_projection)
    cx, cy, cz = camera.position.x, camera.position.y, camera.position.z
    thx, thy, thz = camera.orientation[0], camera.orientation[1], camera.orientation[2]
    ex, ey, ez = camera.surface.x, camera.surface.y, camera.surface.z
    
    x = self.x - cx
    y = self.y - cy
    z = self.z - cz
    
    dx = cos(thy) * (sin(thz) * y + cos(thz) * x) - sin(thy) * z
    dy = sin(thx) * (cos(thy) * z + sin(thy) * (sin(thz) * y + cos(thz) * x)) + cos(thx) * (cos(thz) * y - sin(thz) * x)
    dz = cos(thx) * (cos(thy) * z + sin(thy) * (sin(thz) * y + cos(thz) * x)) - sin(thx) * (cos(thz) * y - sin(thz) * x)
    
    bx = (ez/dz) * dx + ex
    by = (ez/dz) * dy + ey
    
    return (xoffset - bx, by + yoffset)

Here we also begin to see why 3D is so computationally challenging. Even applying this transformation to a single point requires dozens of trigonometric calculations. A complex scene with many thousands of polygons would have to do these calculations many thousands of times per second. This is why GPUs are optimized for parallel processing. With many hundreds or thousands of processor cores specifically optimized for doing this type of math, a GPU can do in a fraction of a second what would take a CPU much longer. However, my 3D engine is not GPU accelerated, meaning that it is orders of magnitudes slower than most 3D engines used to make games these days. Despite this, it is sufficient for the relatively low-poly applications that I use it for.

Now that we can project points into a camera, we have the foundational workings of a 3D graphics engine. From this, we move on to the next step: polygons. Luckily for us, pygame (which I am using to draw the 2D elements to the screen) has built in support for drawing and filling polygons. So, all we need to do in order to draw a polygon is get a list of all its points in 3D space, project them to 2D, and then call pygame to draw to the screen. For our basic polygon class, we can simply define a list of points and a color that we want the polygon to be:

class polygon:
    def __init__(self, pointlist, color):
        self.pointlist = pointlist
        
        self.color = color

Next, we can create a simple method to project all these points and draw to the screen (the x and y offset are for centering the polygon when the window is scaled):

def draw(self, camera, screen, xoffset, yoffset):
    ppoints = []

    for p in self.pointlist:
        ppoints.append(p.project(camera, xoffset, yoffset))

    pygame.draw.polygon(screen, self.color, ppoints)

This works fine in basic cases, however it is easy to see the problems that can arise. This method draws polygons at all times, even if they are behind the camera or out of the camera’s field of view. Not only is this very inefficient, it will also result in the player being able to see everything that is behind them, and could even crash our program if it encounters undefined behavior in pygame’s drawing method. To combat this, we will simply write some code to check if the drawn polygon will be inside the camera’s FOV:

def draw(self, camera, screen, xoffset, yoffset):
    ppoints = []
    insideView = False
    ssize = screen.get_size()

    for p in self.pointlist:
        ppoints.append(p.project(camera, xoffset, yoffset))
        if (ppoints[-1][0] > 0 and ppoints[-1][1] > 0) and (ppoints[-1][0] < ssize[0] and ppoints[-1][1] < ssize[1]):
            insideView = True
    
    if insideView:
        pygame.draw.polygon(screen, self.color, ppoints)

Note that this code will draw a polygon as long as at least one of its points is visible to the camera. This prevents polygons from awkwardly disappearing from the edge of the screen.

Now that we have a way to properly draw polygons to the screen, we need a system for determining how to break objects into polygons. In mathematics, this process is called tessellation. In theory, we could determine the optimal polygon types to tesselate different objects on a case by case basis, but this would introduce a lot of needless complexity into our program. Instead, it is ideal if we can simply choose one type of polygon to tesselate every object. For this purpose, these is no better shape than the triangle. This is due to the simple fact that every polygon can be formed from combinations of triangles, as illustrated below. This process is called polygon triangulation:

So, we will simply add a triangle class that inherits from our polygon class and accepts no more than three points in its contstructor:

class triangle(polygon):
    def __init__(self, p1, p2, p3, color):
        super().__init__([p1, p2, p3], color)

Now that we have a method to project 3D polygons onto our camera and a method to represent objects as tessellations of triangles, we must implement a means of adding objects made up of many triangles to our world. Luckily for us, there is a file type designed for this express purpose: .stl. STL stands, quite fittingly, for Standard Tessellation Language. As the preferred file format for things such as 3D printing, STL files represent objects as collections of many triangles, which is the exact format that our graphics engine uses. Every triangle in an STL file is stored under the following format:

32 bit float * 3 - Normal vector
32 bit float * 3 - Point 1
32 bit float * 3 - Point 2
32 bit float * 3 - Point 3
16 bit short     - Misc. attribute information

The 16 bit attribute information is program-specific, and can be ignored for now. Likewise, the 3 points are simply the three vertices of our triangle and need no further explanation. However, we have a new addition in the form of the normal vector. In mathematics, normal typically just refers to anything that is directly perpendicular to a plane. Therefore, a normal vector is simply a vector that points directly away from the surface of a polygon.

It may seem confusing as to why this information is necessary, however it will become very important when we discuss how we can simulate light interacting with an object. For now, we will simply add a normal parameter to our polygon constructor.

We will also now add an object class to group polygons together to represent larger bodies in the world:

class object:
    def __init__(self, plist, color):
        self.plist = plist #list of polygons in body
        self.color = color
        self.com = point(0,0,0) #center of mass

Much like our polygon class, our object class is currently little more than a list of polygons, though we will add more detailed functionality to it soon. For now though, it is important to mention the center of mass variable that we have added to our object. This stores where the program thinks the center of an object is, which is extremely useful for moving objects around in our world. Much like normal vectors, this will become very important later. Now that we have a way to represent objects, we can create a method to load them from STL files. Below is the code to read from a binary STL into our object:

fdata = open(filename, 'rb').read()
psize = struct.unpack('I', fdata[80:84]) #eat up header and get number of triangles

for i in range(psize[0]):
    entry = struct.unpack('<ffffffffffffH', fdata[84 + 50*i:134 + 50*i])
    self.plist.append(triangle(point(entry[0],entry[1],entry[2]), point(entry[3],entry[4],entry[5]), point(entry[6],entry[7],entry[8]), point(entry[9],entry[10],entry[11]), self.color))
    self.com.x += (entry[3] + entry[6] + entry[9])
    self.com.y += (entry[4] + entry[7] + entry[10])
    self.com.z += (entry[5] + entry[8] + entry[11])

self.com /= (psize[0] * 3)

Now, after adding a simple method to draw all polygons in an object, we theoretically have everything we need to load an object from an STL file and render it in 3D space. Using a low-poly dog model as a test, I added some code in my main file to move the camera’s position and orientation with the keyboard and mouse. Loading the object into the scene gives us the following:

As you can see, we are now able to successfully represent a 3D object in our engine!

So far though, all we are really able to display is a uniformly lit silhouette of an object, which looks unnatural to our human eyes. Everything we see in our world is lit by directional light sources, meaning that how bright a surface looks is a function of how much light is hitting it. This is crucial to our visualization and understanding of 3D objects. Therefore, it is time to add support for lighting to our engine.

In order to implement realistic surface lighting, we need to reintroduce our normal vectors from earlier. The amount of light a surface reflects to the viewer is a function of its angle to a light source. If a surface is perpendicular to the rays of light hitting it, it will appear brightest to the viewer. Likewise, if it is parallel to the source, it will appear to be the dimmest. Normal vectors give us and easy way to determine the angle between a given surface and the rays of light hitting it through use of the dot product. In vector math, the dot product of two given vectors is as follows:

\(\Large v_a \cdot v_b = \sum_{i=1}^{n} a_i \cdot b_i + a_{i+1} \cdot b_{i+1} + … a_{n} \cdot b_{n} = ||v_a|| \cdot ||v_b|| \cos(\theta) \)

Since we are only ever going to be working with vectors in 3D space, we can create a specific implementation to operate on coordinate vectors in our engine:

def dotProduct(a, b):
    return (a.x * b.x) + (a.y * b.y) + (a.z * b.z)

Notice how the definition above holds the dot product of two vectors to be equivalent to the product of the magnitudes of the vectors multiplied buy the cosine of the angle between them. Therefore, we simply need to isolate this term to find the angle between our polygon and the rays from our point source.:

\(\Large \theta = \arccos\left(\frac{n \cdot l}{|n| |l|}\right)\)

Hence, our full point source class in implemented as follows (the square root of the dot product is equivalent to taking the magnitude of a vector):

class pointSource: #point source of light for shading
    def __init__(self, pos):
        self.pos = pos #point object
        
    def getAngle(self, triangle): #get angle between surface normal and point source
        dv = triangle.getcom() - self.pos
        n = triangle.normal
        
        return acos(dotProduct(n, dv)/(sqrt(dotProduct(dv, dv)) * sqrt(dotProduct(n, n)))) #return angle

Now that we have a means of calculating the interactions between each light source and each surface, we’ll add the following code to the polygon drawing method:

if insideView:
    tcolor = self.color
    if (shaders): #apply shaders
        scalar = 0
        
        for shader in shaders:
            sangle = -(cos(shader.getAngle(self)) / 2)
            
            if sangle >= 0:
                scalar += sangle
        
        scalar += 0.5
        
        if scalar < 0.5:
            scalar = 0.5
            
        tcolor = (floor(self.color[0] * scalar), floor(self.color[1] * scalar), floor(self.color[2] * scalar))
    
    pygame.draw.polygon(screen, tcolor, ppoints)

This will scale the color of each polygon between 100% and 50% of its original brightness depending on how much light is hitting it from the sum of every point source. Now that we can simulate light, we’ll run our program again. It seems to be working on an individual basis, but once we load our dog model from last time it’s clear to see that something is wrong:

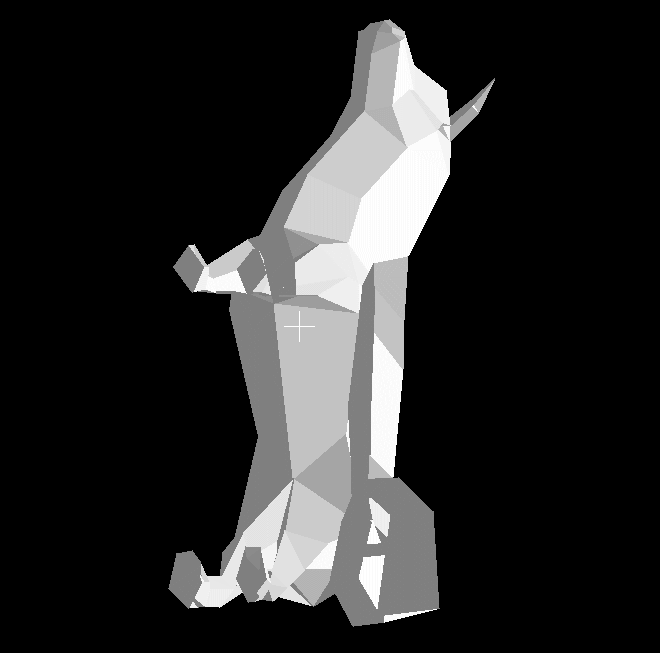
While the head of the dog appears to be shaded correctly in response to our point source, something very odd is happening with the rest of its body. There are noticeable dark spots to the right of its torso and tail that seem to break all laws of perspective and don’t fit in with the lighting of the rest of the model. The same is true for various other smaller spots such as the front paws. The reason for this is very simple: our polygons are not being drawn in order.

In the real world, it is a basic fact of life that objects closer to the viewer obscure those that are farther away, but nothing can be taken for granted here. Because we simply imported our polygons in the order they were in the STL file, it is possible for objects farther away from the camera to obscure closer objects. To fix this, we must sort all the polygons in a given scene by distance and draw them in order using something called the painter’s algorithm.

The painter’s algorithm is the most basic way of solving this problem in 3D graphics. In order to implement it, we need to calculate the center of mass of every polygon and then use the 3D distance formula to sort them such that the furthest polygons are drawn first and the closest polygons are drawn last. This should not be done on a object-by-object basis to account for the scenarios in which objects may overlap or clip one another. It is implemented in the scene class here:

def drawPaintedRaster(self): #painter's algorithm
    numdrawn = 0
    
    for object in self.objects:
        for p in object.plist:
            p.getDistance(self.camera)
            
    self.polygons.sort(key = lambda x: x.distance, reverse = True) #python's sort method is faster than inorder insertion
 
    for polygon in self.polygons: #draw in order after storting 
        numdrawn += polygon.drawRaster(self.camera, self.screen, int(self.screen.get_width()/2), int(self.screen.get_height()/2), self.lightSources)
    
    return numdrawn

Now that we can draw polygons in depth order, we can run our program with the dog model again to see the following:

Here it is clear to see that the model is interacting with the light source as we would expect, with the right side of its body illuminated more than its left. There are a few noticeable artifacts on its right ear and legs which are caused by the fact that the centers of mass of some outlier polygons are closer to the camera than those of the polygons that should obscure them. This problem could be solved with more advanced techniques such as Z-buffering, although it is a small enough issue here that this solution is sufficient.

Now that we can load and light objects somewhat realistically, we should now add some methods for translating and rotating them about in the scene.

In order to move an object, we must of course displace every polygon belonging to the object by the same amount in order to retain the object’s exact shape. First, we will add a move method to the polygon class that will move every point and the polygon’s center of mass by the same amount. After this, we can simply call this move method on every polygon in our object to translate it anywhere in our world:

def translate(self, offset): #offset should be a point object
    self.com += offset #move center of mass with offset
    for p in self.plist:
        p.move(offset)

Note that translation is based on an offset from the object’s current location, and not absolute coordinates. If we input a movement by 0.1 in the x direction every frame, we get the following:

Now that we can translate objects in our world, the last major step we need to take in order to have a basic fully-featured 3D engine is the implementation of rotation. To rotate objects in 3D space, we once again must turn to linear algebra. Unfortunately, there is no general formula for a rotation in an arbitrary direction about an arbitrary axis at any point in space, so instead we must use the following three transformations for rotations about the three XYZ axes:

These are implemented in the polygon class as follows. We must also transform the normal vectors of each polygon to align with their new orientations:

def getcom(self): #set center of mass
    self.com = averageOfPoints(self.pointlist)
    return self.com
    
def rotateX(self, angle): #rotate about X-axis (requires translation to maintain position)
    self.normal = point(self.normal.x, float(self.normal.y * cos(angle) - self.normal.z * sin(angle)), float(self.normal.y * sin(angle) + self.normal.z * cos(angle)))
    for p in self.pointlist:
        ny = float(p.y * cos(angle) - p.z * sin(angle))
        nz = float(p.y * sin(angle) + p.z * cos(angle))
        
        p.y = ny
        p.z = nz
        
    self.getcom()
        
def rotateY(self, angle):
    self.normal = point(float(self.normal.x * cos(angle) + self.normal.z * sin(angle)), self.normal.y, float(self.normal.z * cos(angle) - self.normal.x * sin(angle)))
    for p in self.pointlist:
        nx = float(p.x * cos(angle) + p.z * sin(angle))
        nz = float(p.z * cos(angle) - p.x * sin(angle))
        
        p.x = nx
        p.z = nz
        
    self.getcom()
        
def rotateZ(self, angle):
    self.normal = point(float(self.normal.x * cos(angle) - self.normal.y * sin(angle)), float(self.normal.x * sin(angle) + self.normal.y * cos(angle)), self.normal.z)
    for p in self.pointlist:
        nx = float(p.x * cos(angle) - p.y * sin(angle))
        ny = float(p.x * sin(angle) + p.y * cos(angle))
        
        p.x = nx
        p.y = ny

    self.getcom()

Because all these transformations are defined about their respective axes, they will not rotate an object in place unless its center of mass is located exactly at the origin. So, in order to solve this problem, we will simply translate an object to the origin, apply all rotations, and then translate it back to its original location before the next frame is drawn. This may seem somewhat hacky, but it is in fact the main strategy that simple graphics engines use for transformations. More modern solutions involve quaternions to avoid gimbal lock, but that is outside the scope of this project for the time being. The code for rotations in the object class is as follows:

def rotate(self, angles): #arg should be array or tuple of three values
    for p in self.plist:
        p.move(point(-self.com.x,-self.com.y,-self.com.z)) #move center of mass to origin
        p.rotateX(angles[0])
        p.rotateY(angles[1])
        p.rotateZ(angles[2])
        p.move(point(self.com.x,self.com.y,self.com.z)) #move back

Finally, we will apply a rotation of 0.025 radians per frame in each axis to our dog model:

Now our 3D engine is more or less feature-complete. It is now possible for us to create and animate entire scenes with multiple objects that can be lit, translated, and rotated in the world. Before concluding this article, I should make mention of some of its limitations. Because the engine uses only Python and Pygame for all its drawing functions, there is absolutely no hardware acceleration, meaning that the CPU is doing all the graphics calculations, which it is certainly not optimized for. Due to this, the framerate drops significantly when polygon counts exceed around 200 or whenever rotations are being applied to objects with more than a couple dozen polygons. If I were to attempt to use this engine to make an actual game of any sort (other than 3D Tic Tac Toe), it would almost certainly not be up to the task performance-wise.

I have plans to port this engine to C++ and CUDA in order to rapidly increase engine performance, however I currently am too involved with school and other projects to do so. If I ever do end up making a complex 3D game, it will likely be in this future version.